Contributors: Stas Fainer, Yi-Ting Tu
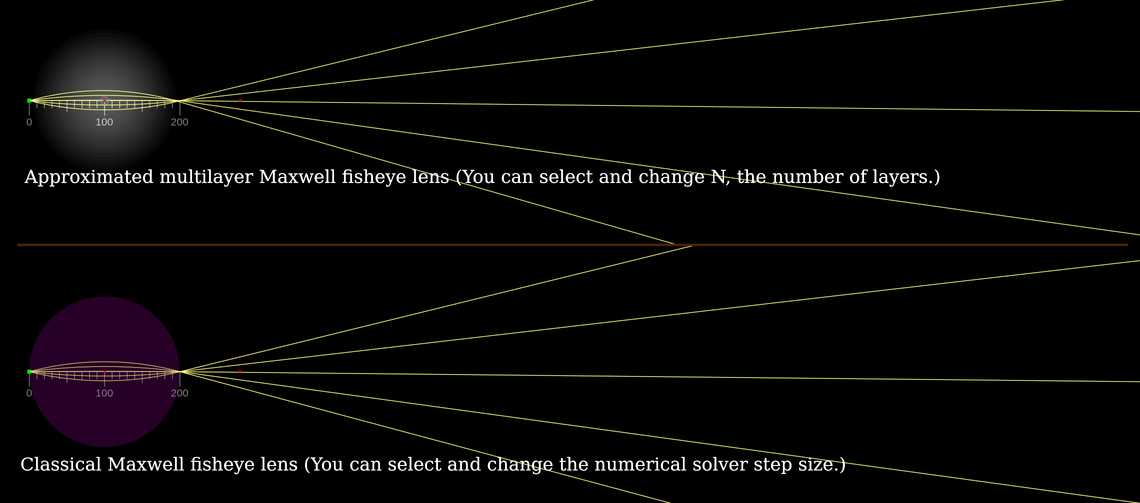
This is a simulation of a Maxwell fish-eye lens, which is a spherical dielectric with refractive index \(n(r) = \frac{n_0}{1+(\frac{r}{R})^2} \), where \(n_0=2\) is the refractive index in the center of the lens, \(R=100\) is the radius of the lens, and \(r\) is the radial distance from the center of the lens.
The top dielectric is composed of \(N=20\) concentric spherical lenses with radius \(R_i=5(N+1-i)\) and refractive index \(n_i = \frac{n_0}{1+(\frac{R_i}{R})^2} \), where \(i=1,\ldots,N\). However, since this simulator calculates the effective refractive index of an optical element by multiplying the element's numerical refractive index with the numerical refractive indices of the optical elements which are embedded within it, the numerical refractive index of the \(i\)th concentric spherical lens is given by \(n_{i}^\text{numerical}=\frac{n_i}{n_{i-1}}\).
The bottom dielectric is a gradient-index material with the refractive index \(n(r)\).