Aplanatic points

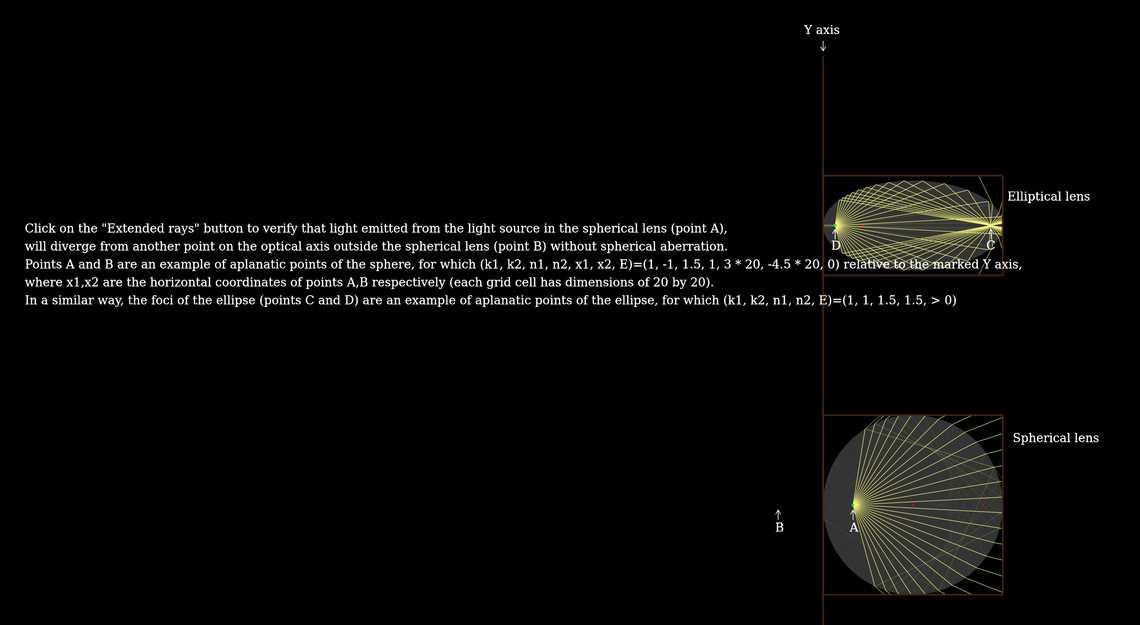
Aplanatic points of an optical system are special points on its optical axis, such that "rays proceeding from one of them will all converge to, or seen to diverge from the other point".

• Ellipse: the two foci of the elliptical lens/mirror are aplanatic points, since light emitted from one focus will converge towards the other.
• Sphere: a spherical lens has two aplanatic points, inside and outside the sphere - for more details see the simulation.
• Hyperbola: the two foci of the Hyperbolic mirror simulation are also aplanatic points.

Given two points with horizontal coordinates \(x_1\) and \(x_2\), identical vertical coordinates, and given the refractive index outside and inside our optical element as \(n_1\) and \(n_2\) (respectively), for this two points to be aplanatic points, the boundary of our optical element must fulfill\begin{equation}k_1 n_1 \sqrt{ (x - x_1)^2 + y^2} + k_2 n_2 \sqrt{ (x - x_2)^2 + y^2} = E\end{equation}such that \(k_i=1\) or \(-1\) if the ray connecting \(x_i\) and the boundary of our optical element is real or imaginary, respectively, and \(E\) is a constant for which this equation has a non-trivial solution. This equation (which can be derived using Fermat's principle) is an equation of a Cartesian oval, of which the conic sections are special cases.