Punkty aplanatyczne

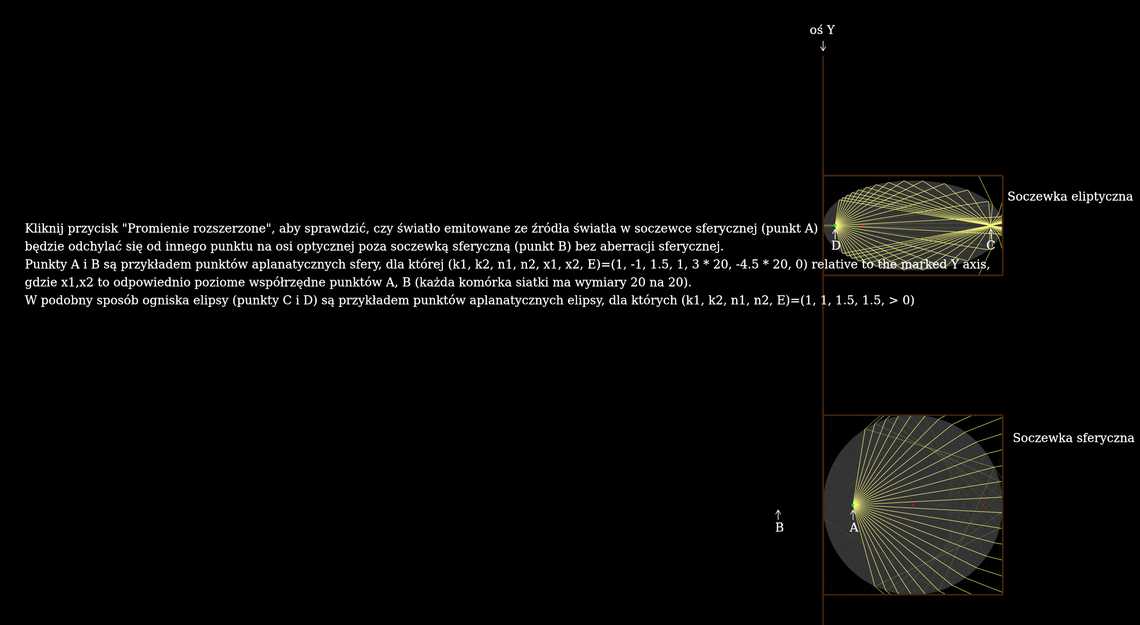
Punkty aplanatyczne układu optycznego to szczególne punkty na jego osi optycznej, takie, że "promienie wychodzące z jednego z nich zbiegają się lub rozchodzą się z drugiego punktu".

• Elipsa: dwa ogniska eliptycznej soczewki/zwierciadła są punktami aplanatycznymi, ponieważ światło emitowane z jednego ogniska zbiega się w kierunku drugiego.
• Sfera: soczewka sferyczna ma dwa punkty aplanatyczne, wewnątrz i na zewnątrz kuli - więcej szczegółów w symulacji.
• Hiperbola: dwa ogniska modelu zwierciadła hiperbolicznego są również punktami aplanatycznymi.

Jeśli dane są dwa punkty o odciętych \(x_1\) i \(x_2\) oraz identycznych rzędnych, i współczynniki załamania światła na zewnątrz i wewnątrz naszego elementu optycznego wynoszą odpowiednio \(n_1\) i \(n_2\), to aby te dwa punkty były punktami aplanatycznymi, granica naszego elementu optycznego musi spełniać równanie\begin{equation}k_1 n_1 \sqrt{ (x - x_1)^2 + y^2} + k_2 n_2 \sqrt{ (x - x_2)^2 + y^2} = E\end{equation}, gdzie \(k_i=1\) or \(-1\), jeśli promień łączący \(x_i\) i granicę naszego elementu optycznego jest odpowiednio rzeczywisty lub pozorny, a \(E\) jest stałą, dla której to równanie ma nietrywialne rozwiązanie. To równanie (które można wyprowadzić za pomocą zasady Fermata) jest równaniem owalu Kartezjusza, którego krzywe stożkowe są przypadkami szczególnymi.