Logarithmic spiral ray path

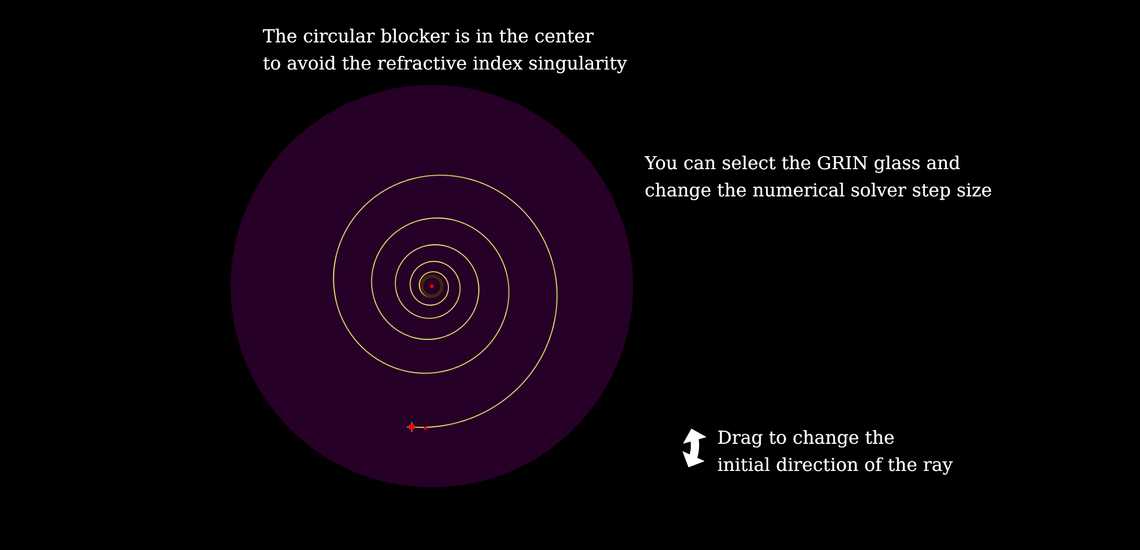
The refractive index function that supports logarithmic spiral ray paths is of the form \(r(θ) = r_0\,e^{-k\theta}\), where \(r_0,k > 0\) and \(\alpha = \arctan k\) is a constant angle between the two tangents at the intersection point between the concentric logarithmic spiral and circle (as demonstrated in this animation), is \(n(r) ∝ \frac{1}{r} \) (this can be shown by writing the optical path in polar coordinates, and using Fermat's principle).