Symulacja biegu promieni
Osoba wnosząca wkład: Stas Fainer
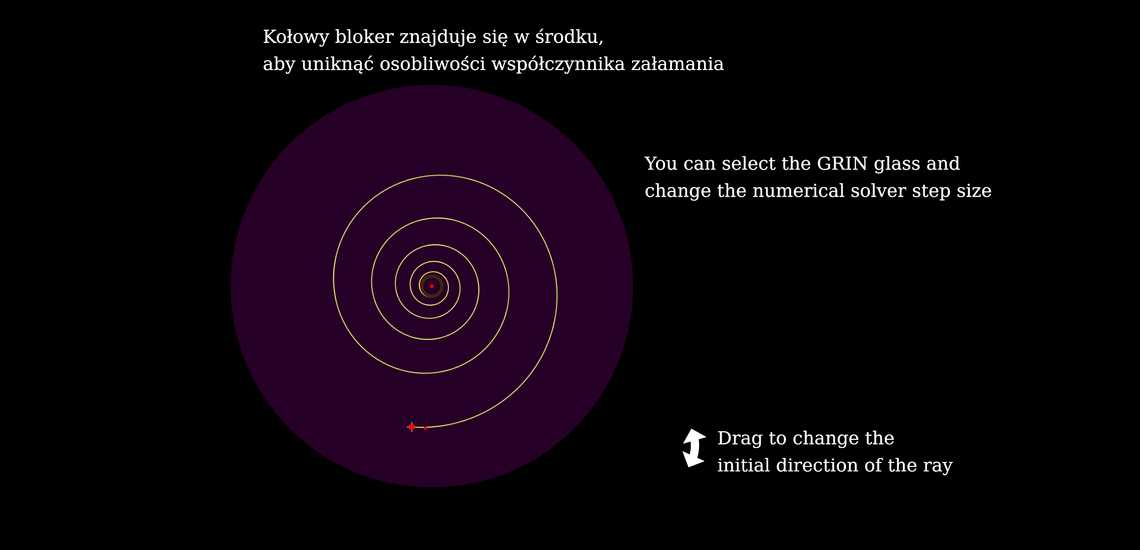
Funkcja współczynnika załamania światła, która wspiera promienie o torach spirali logarytmicznych o postaci \(r(θ) = r_0\,e^{-k\theta}\), gdzie \(r_0,k > 0\) i \(\alpha = \arctan k\) to stały kąt między dwiema stycznymi w punkcie przecięcia koncentrycznej spirali logarytmicznej z okręgiem (jak pokazuje ta animacja), to \(n(r) ∝ \frac{1}{r}\) (można to wykazać zapisując ścieżkę optyczną we współrzędnych biegunowych i wykorzystując zasadę Fermata).
