Caminho de raios em espiral logarítmica

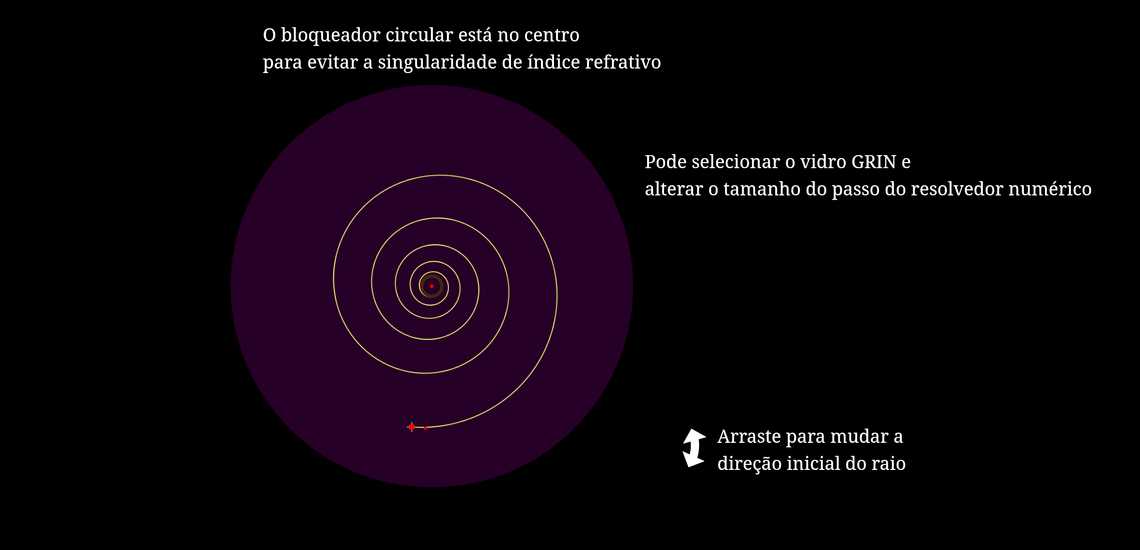
A função de índice refrativo que suporta caminhos de raio de espiral logarítmica é da forma \(r(θ) = r_0\,e^{-k\theta}\), onde \(r_0,k > 0\) e\(\alpha = \arctan k\) é um ângulo constante entre as duas tangentes no ponto de interseção entre a espiral logarítmica concêntrica e círculo(como demonstrado nessa animação) é \(n(r)\propto\frac{1}{r} \) (isto pode ser demonstrado escrevendo o caminho óptico em coordenadas polares e usando o princípio de Fermat).