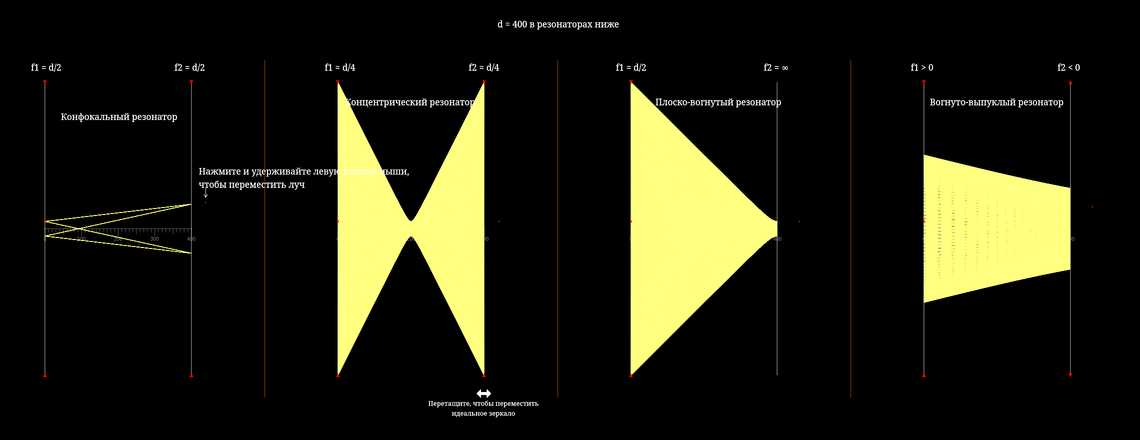
участник:Stas Fainer
Это моделирование лучей внутри оптической полости с двумя зеркалами. Учитывая, что длина полости равна \(d\), а радиус кривизны ее зеркал равен \(R_1\) и \(R_2\) соответственно (с соглашением, что \(R>0\) для вогнутого зеркала), то оптическая полость является устойчивой (это означает, что для каждого луча, который исходит от одного из зеркал к другому зеркалу, для достаточно высоких зеркал гарантируется нерасходящаяся траектория), тогда и только тогда, когда \(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\). В этом моделировании мы предполагаем, что зеркала являются идеальными изогнутыми зеркалами, что означает, что \(f=\frac{R}{2}\), что приводит предыдущее условие устойчивости к \(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\). Здесь — это аналогичное моделирование со сферическими зеркалами, где первое условие устойчивости выполняется в параксиальном приближении.