Wnęka optyczna z dwoma zwierciadłami

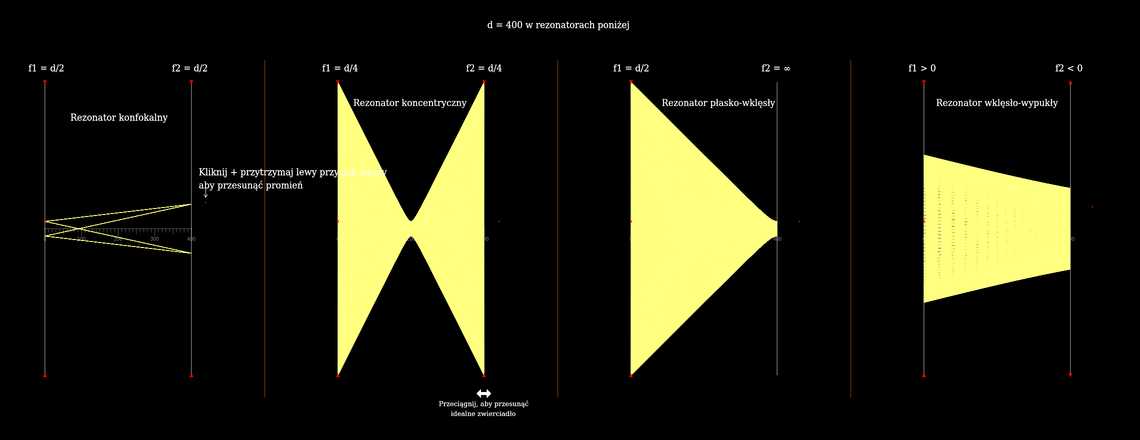
Jest to symulacja promieni wewnątrz wnęki optycznej z dwoma zwierciadłami. Biorąc pod uwagę, że długość wnęki wynosi \(d\), a promienie krzywizny jej zwierciadeł wynoszą odpowiednio \(R_1\) i \(R_2\) (z konwencją, że \(R>0\) dla zwierciadła wklęsłego), to wnęka optyczna jest stabilna (co oznacza, że dla każdego promienia wychodzącego z jednego zwierciadeł w kierunku drugiego zwierciadła trajektoria nierozbieżna jest gwarantowana dla dostatecznie wysokich zwierciadeł), wtedy i tylko wtedy, gdy \(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\). W tej symulacji zakładamy, że zwierciadła są idealnie zakrzywionymi zwierciadłami, co oznacza, że \(f=\frac{R}{2}\) i sprowadza poprzedni warunek stabilności do postaci \(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\). Tutaj podobna symulacja ze zwierciadłami sferycznymi, gdzie pierwszy warunek stabilności jest spełniony w przybliżeniu przyosiowym.