Two-mirror optical cavity

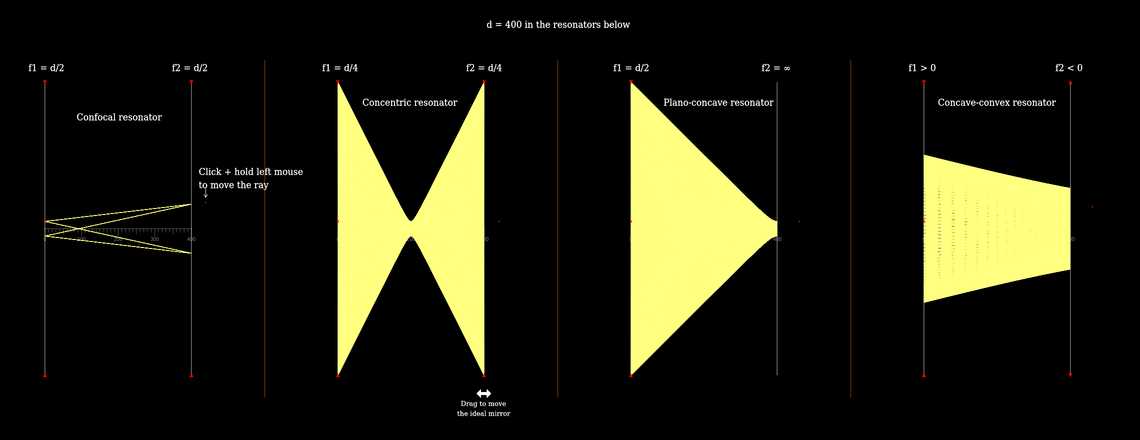
This is a simulation of rays inside an optical cavity with two mirrors. Given the length of the cavity is \(d\), and the radius of curvature of its mirrors is \(R_1\) and \(R_2\) respectively (with the convention that \(R>0\) for a concave mirror), then the optical cavity is stable (meaning that for each ray that emanates from one of the mirrors towards the other mirror, a non-divergent trajectory is guaranteed for sufficiently high mirrors), if and only if \(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\). In this simulation we assume that the mirrors are ideal curved mirrors, meaning that \(f=\frac{R}{2}\), rendering the previous stability condition to \(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\). Here is a similar simulation with spherical mirrors, where the first stability condition holds in the paraxial approximation.