雙鏡共振腔

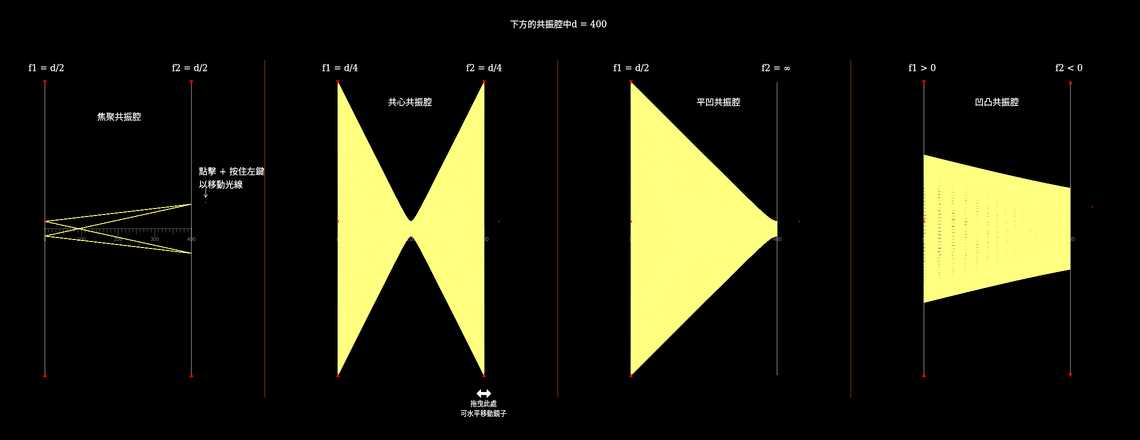
模擬由兩面鏡子組成的共振腔。假設腔體的長度為\(d\)，其鏡子的曲率半徑分別為\(R_1\)和\(R_2\)（根據慣例，\(R>0\)為凹面鏡），那麼只有當\(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\)時，共振腔才會穩定（這意味著從一面鏡子向另一面鏡子發出的每一道光線都保證有非發散的軌跡，前提是鏡子的反射率足夠高）。在此模擬中，我們假設鏡子是理想曲面鏡，這意味著\(f=\frac{R}{2}\)，將先前的穩定條件變為\(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\)。這裡有一個使用球面鏡的類似模擬，在抛物面近似下，第一種穩定條件成立。