Cavidade óptica de dois espelhos

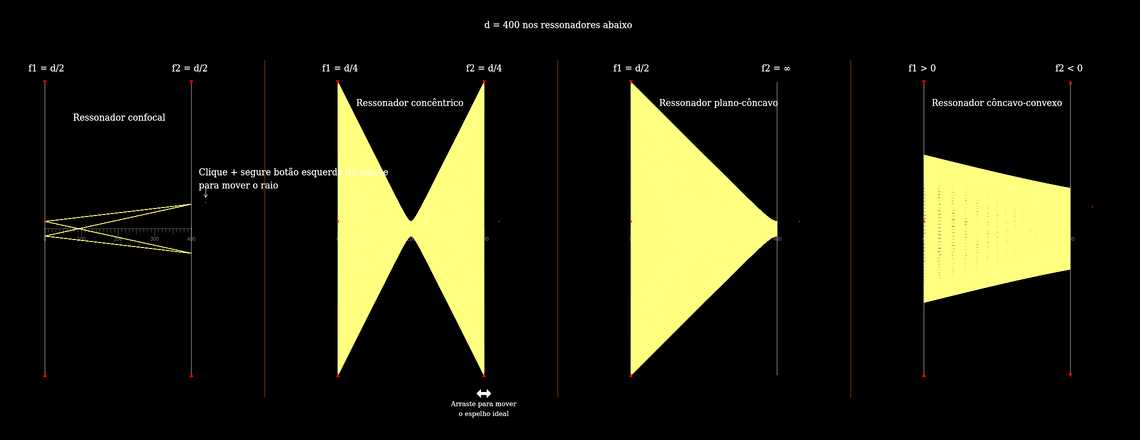
Essa é uma simulação de raios dentro de uma cavidade óptica com dois espelhos. Dado o comprimento da cavidade \(d\), e o raio de curvatura de seus espelhos \(R_1\) e \(R_2\) respectivamente (com a convenção que \(R>0\) para um espelho côncavo), a cavidade óptica é estável (o que quer dizer que para cada raio que sai de um dos espelhos rumo ao outro, uma trajetória não-divergente é garantida para espelhos suficientemente altos) se, e somente se, \(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\). Nessa simulação nós assumimos que os espelhos são curvos ideais, o que significa que \(f=\frac{R}{2}\), fazendo com que a condição de estabilidade anterior seja \(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\). Esta é uma simulação similar com espelhos esféricos, onde a primeira condição de estabilidade é verdade na aproximação paraxial.