Cavité optique à deux miroirs

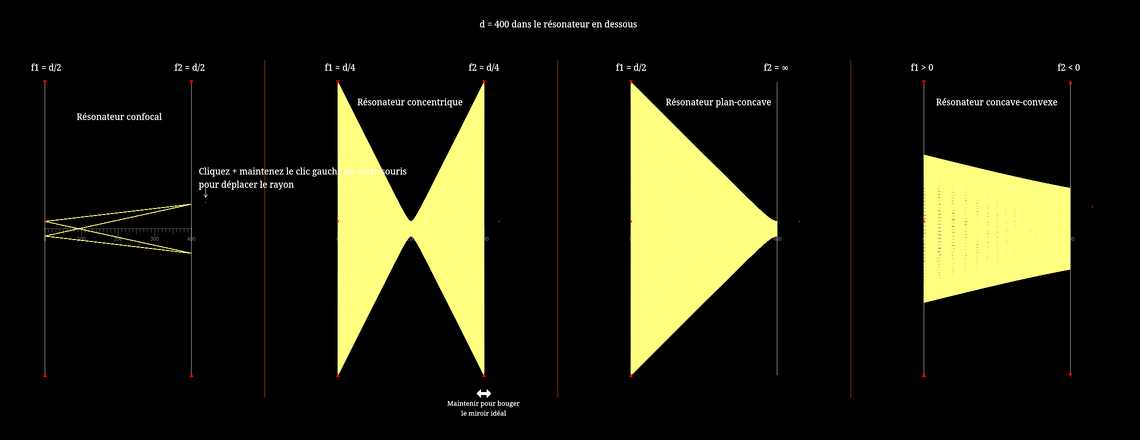
Il s'agit d'une simulation des rayons à l'intérieur d'une cavité optique comportant deux miroirs. Étant donné que la longueur de la cavité est \(d\) et que le rayon de courbure de ses miroirs est respectivement \(R_1\) et \(R_2\) (avec la convention que \(R>0\) pour un miroir concave), alors la cavité optique est stable (ce qui signifie que pour chaque rayon qui émane d'un des miroirs vers l'autre miroir, une trajectoire non divergente est garantie pour des miroirs suffisamment hauts), si et seulement si \(0\leq (1-\frac {d}{R_1})(1-\frac {d}{R_2})\leq 1\). Dans cette simulation, nous supposons que les miroirs sont des miroirs courbes idéaux, ce qui signifie que \(f=\frac{R}{2}\), ce qui donne la condition de stabilité précédente \(0\leq (1-\frac {d}{2f_1})(1-\frac {d}{2f_2})\leq 1\). Ici se trouve une simulation similaire avec des miroirs sphériques, où la première condition de stabilité est valable dans l'approximation paraxiale.